A major issue with the xbar and r chart formula is that if a process has between subgroup variability that is common cause false, special cause signals can often occur. This is an important concept that everyone who uses xbar and r charts should understand but typically don’t. A 30,000-foot-level metric tracking approach not only gets around this problem but also provides a process capability statement (in one chart).
The described Xbar and R chart formula issues and resolution concepts can be used to help organizations not only determine how to improve time-series manufacturing data examination but measurements throughout their organization.
Xbar and R Chart Formula Issues and Resolution
Content of this webpage is from Chapter 12 of Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Forrest W. Breyfogle III.
Xbar and R charts are used in quality control to identify when special cause or out-of-control conditions occur in time-series data so that timely corrective actions can be taken to resolve problems. Sometimes data from a statistical process control (SPC)  and R control chart are used also to provide a process capability relative to product specification requirements.
and R control chart are used also to provide a process capability relative to product specification requirements.
However, there are formula issues in how  and R control charts are often created and applied. Related process capability statements can have issues, too.
and R control charts are often created and applied. Related process capability statements can have issues, too.
The application shortcoming of  and R control charts will be described in this article along with an alternative 30,000-foot-level charting methodology that not only addresses these issues but enhances application of the techniques. The described methodology not only improves the accuracy of common-cause and special-cause statements but also provides a better and more easily understandable process capability or process performance statement that is predictive.
and R control charts will be described in this article along with an alternative 30,000-foot-level charting methodology that not only addresses these issues but enhances application of the techniques. The described methodology not only improves the accuracy of common-cause and special-cause statements but also provides a better and more easily understandable process capability or process performance statement that is predictive.
Traditional xbar and r chart Formula Illustration
When examining time-series data, we would like the most appropriate action or non-action to occur. However, the conclusion of what action or non-action to take can be a function of how the data are examined. This point will be illustrated using the data in Table 11, which contains the magnitude of a continuous response from five samples that had a daily subgrouping.
This data could be the completion time for five randomly-selected daily procedural transactions in an insurance company, hospital, or one-shift manufacturing facility. In the following analyses, focus will be given initially to the assessment of process stability and then, if stable, its process capability relative to customer specifications of 95 to 105.
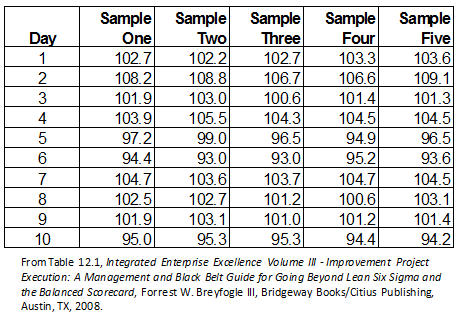
Table 1: Time-series Data
A standard statistical control chart guide, based on Walter Shewhart’s guidelines 2,3, would recommend using an  and R control chart for assessing the stability of the process, as illustrated in Figure 1.
and R control chart for assessing the stability of the process, as illustrated in Figure 1.
Some courses may teach that you should not generate a control chart with only ten subgroups, which is intended to reduce the uncertainty of the standard deviation estimate, but having fewer than 25 subgroups or data points will only reduce the chance of detecting an out-of-control condition. Using a smaller number of data points in a control chart increases a beta-risk equivalent, where a true out-of-control condition may not be detected. Smaller sample control charts that show an out-of-control condition should still be investigated, since it is likely that an out-of-the-norm event occurred, given underlying assumptions used to create the chart.
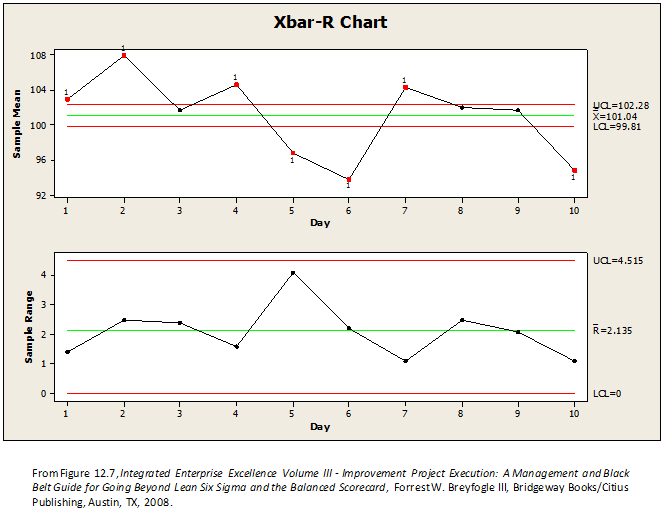
Figure 1: Traditional x-bar and R Control Chart
Whenever a value on a control chart is beyond the upper control limit (UCL) or lower control limit (LCL), the process is said to be out of control. Out-of-control occurrences are called special-cause conditions and can trigger a causal problem investigation. Since so many out-of-control conditions are apparent in Figure 1, causal investigation would be occurring very frequently. In addition, no process capability statement should be made about how this unstable process is expected to perform relative to its specification limits.
The  chart in Figure 1 is out of control; however, if one were to step back and look at the
chart in Figure 1 is out of control; however, if one were to step back and look at the  chart alone, it does look like the process would continue to produce mean values within the boundaries of the displayed chart axes; i.e, 92 to 108. If the process shows the average values ranging from 92 to 108 over the next ten or 20 subgroups, should we consider the process stable? If we ignore the control chart definition of stable and replace it with the word “consistent”, then we could consider that the process is consistent.
chart alone, it does look like the process would continue to produce mean values within the boundaries of the displayed chart axes; i.e, 92 to 108. If the process shows the average values ranging from 92 to 108 over the next ten or 20 subgroups, should we consider the process stable? If we ignore the control chart definition of stable and replace it with the word “consistent”, then we could consider that the process is consistent.
If the process subgroup means are consistent over time, and the  and R chart identifies the process as out of control, or inconsistent, what is wrong? Maybe nothing is wrong. An
and R chart identifies the process as out of control, or inconsistent, what is wrong? Maybe nothing is wrong. An  and R chart was created by Walter Shewhart to identify any “assignable” cause that causes the process mean to change so that a process operator may adjust the process to return the process mean to the historic values. This is a good question to ask of a single process in order to provide a control signal that drives an adjustment to the process. But it is not the best question to ask when a business wants to assess the overall performance of its business process relative to customer needs.
and R chart was created by Walter Shewhart to identify any “assignable” cause that causes the process mean to change so that a process operator may adjust the process to return the process mean to the historic values. This is a good question to ask of a single process in order to provide a control signal that drives an adjustment to the process. But it is not the best question to ask when a business wants to assess the overall performance of its business process relative to customer needs.
What is an appropriate generic sampling and control-charting approach that would provide a high-level business and/or customer view of a process output, noting that this response may need to include performance differences between worker shifts, equipment, and/or locations? The customer or the business does not care how a process is executed; each expects the process output to be acceptable no matter how it was conducted. I refer to an assessment that addresses these needs as a 30,000-foot-level view (not unlike examining the terrain below from an airplane in flight at 30,000 feet, i.e., a high-level perspective of the terrain below).
Xbar and R chart Formula Problems and Resolution using 30,000-foot-level Charting
For the  chart portion of the
chart portion of the  and R control chart pair, the UCL and LCL are calculated from the relationships
and R control chart pair, the UCL and LCL are calculated from the relationships

where  is the overall average of the subgroups, A2 is a constant depending upon subgroup size, and
is the overall average of the subgroups, A2 is a constant depending upon subgroup size, and  is the average range within subgroups.
is the average range within subgroups.
For reference, an X chart from an XmR chart pair, the UCL and LCL are calculated from the relationships

where  is the average moving range between subgroups.
is the average moving range between subgroups.
The limits for the  chart of an
chart of an  and R chart pair are derived from within-subgroup variability (
and R chart pair are derived from within-subgroup variability ( ), while sampling standard deviations for the X chart of an XmR chart pair are calculated from between-subgroup variability (
), while sampling standard deviations for the X chart of an XmR chart pair are calculated from between-subgroup variability ( ).
).
The implication of this difference in control-chart calculations is that, if there is a large natural-process variance component between subgroups, this variability could result in out-of-control signals for an  and R control chart, while an XmR chart of the same situation could indicate an in-control process.
and R control chart, while an XmR chart of the same situation could indicate an in-control process.
Control charts only address process stability, not performance relative to customer needs/desires. Process capability/performance statements can provide this form of insight when a process is stable. For processes that have a specification, typical process-capability statements are provided using process-capability indices such as Cp, Cpk, Pp and Ppk.4 However, the interpretation of these indices relative to how a process is performing relative to customer needs can be confusing and deceptive in that reported values can be a function of how samples are drawn from the process.
What is needed to address this potential sampling plan inconsistency is a consistent approach where the impact from this common-cause input noise occurs between subgroupings; e.g., day, week, or month. I refer to the sampling plan that accomplishes this as infrequent sub-grouping/ sampling and this process assessment perspective as a 30,000-foot-level view; i.e., as stated previously, not unlike an airplane’s high-level view of the earth. When creating control charts at the 30,000-foot-level, we need to include between-subgroup variability within our control-chart limit calculations. What is also needed is a report-out of how a process is performing relative to customers’ needs that is easier to understand than typical process-capability statements.
To address this customer-performance reporting in words that are easily understood, a 30,000-foot-level assessment provides, in addition to a process-stability assessment, a percentage non-conformance rate is provided when there is a specification, as Figure 2 illustrates using a probability plot.
For this randomly-generated data set that had both a within-and between-subgroup variance component, a conclusion from the two control charts is that the process is stable. The probability plot’s null hypothesis test of data normality is rejected at a level of 0.05 since the reported probability plot p-value is less than 0.05; however, visually, the best estimate line in the probability plot appears close enough to straight that a rough estimate for non-conformance could be reported in terms that everyone can easily understand; i.e., about 27% non-conformance.
In Figure 2’s control-chart pair, it could also be noted how within-subgroup stability was assessed over time using a log transformation of standard deviation; i.e., Box-Cox transformation with lambda = 0. Since standard deviation cannot be less than zero, a log-normal transformation can, in general, be used to model the skewness of this within-subgroup variability’s distribution for 30,000-foot-level reporting.
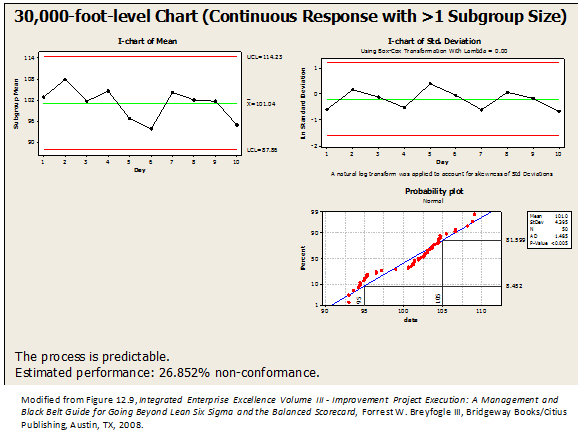
Figure 2: 30,000-foot-level Chart5
Summary: Xbar and R Chart Formula Problem Resolved
For the presented data, the 30,000-foot-level report-out changed how one would view the process’ performance from considering that the process was not stable using a traditional  and R control chart to a process that has a non-compliance rate of about 27%, when assessing the process at the 30,000-foot-level. This approximate unacceptability rate can be expected in the future unless something changes. To improve a process’ common-cause level of performance when reported at the 30,000-foot-level, the process needs to be enhanced; e.g., through a Lean Six Sigma improvement project.
and R control chart to a process that has a non-compliance rate of about 27%, when assessing the process at the 30,000-foot-level. This approximate unacceptability rate can be expected in the future unless something changes. To improve a process’ common-cause level of performance when reported at the 30,000-foot-level, the process needs to be enhanced; e.g., through a Lean Six Sigma improvement project.
A Free Software App for Creating 30,000-foot-level charts
30,000-foot-level Charting Applications
The described 30,000-foot-level reporting technique has many applications beyond X-bar and R control chart issues and resolution.
Organizations benefit when they transform their scorecard and dashboard reporting to 30,000-foot-level predictive performance metrics, which could be reported throughout an organization.
An Integrated Enterprise Excellence (IEE) Business Management System with its 30,000-foot-level predictive-scorecard reporting addresses the traditional scorecard and improvement issues that are described in a 1-minute video:
30,000-foot-level charting can reduce the firefighting that can occur with traditional business scorecarding systems.The Integrated Enterprise Excellence (IEE) business management system uses 30,000-foot-level charting to address these issues.

References
- Forrest W. Breyfogle III, Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Bridgeway Books/Citius Publishing, 2008
- W. A. Shewhart, Economic Control of Quality of Manufactured Product, D. Van Nostrand Co., New York, 1931.
- W. A. Shewhart, Statistical Method from the Viewpoint of Quality Control, United States Department of Agriculture, 1939.
- Statistical Process Control (SPC) Reference Manual, Second edition, Chrysler Corporation, Ford Motor Company, General Motors Corporation, AIAG, 1995
- 30,000-foot-level figure created using 30,000-foot-level free app
Application of IEE to Creation of a Long-lasting Business Process Management (BPM) and Management Information System (MIS) Implementation
How to benefit from the IEE system and with application of 30,000-foot-level charting with its Enterprise Performance Reporting System (EPRS) software (which provides predictive scorecard reporting that is automatically updated and a process improvement system so the big picture benefits) is described in:
- How to Avoid Commonplace Business Management System Software Problems
- How to Avoid Commonplace Management Information System Software Problems
- How to Avoid Commonplace Business Process Management Software Problems
- How to Avoid Commonplace Lean Six Sigma Problems
Next Steps
- Schedule a video meeting session with Forrest through the link https://smartersolutions.com/schedule-zoom-session/

