Transforming individuals control chart data is an important consideration to avoid common cause variability appearing as special cause events. The transformation of data (for situations that make physical sense) is easily accomplished in 30,000-foot-level tracking metric report-outs, which also can provide a predictive process capability statement — in one chart.
The Integrated Enterprise Excellence (IEE) Business Management System provides a means to integrate 30,000-foot-level futuristic metric reporting with the processes that created them.
Operational Excellence (OE), according to a past Wikipedia definition, is to create a system for sustainable improvement of key performance metrics. To achieve this Wikipedia OE directive, measurements need to be tracked from a process-output point of view. These metrics also need to be structurally linked to the processes that created them. An Operational Excellence System for achieving these OE objectives is Integrated Enterprise Excellence.
Operational Excellence System with 30,000-foot-level Measurement Report-outs
Note: The content below is from Chapter 12 of Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Forrest W. Breyfogle III.
The IEE 30,000-foot-level reporting format provides a structured methodology for examining a process output response from a high level point of view. The creation of these metrics involve a two-step process:
- Determine process stability (from a 30,000-foot-level perspective)
- Create a capability/performance statement that describes how the process is not only currently performing but expected to perform in the future.
If the stable-process-prediction-statement is unsatisfactory, this metric improvement needs pulls for a process enhancement effort; e.g., Lean Six Sigma process improvement project.
A 30,000-foot-level individuals chart is used to assess process stability; however, this chart is not robust to data non-normality. Because of this chart characteristic, data may need to be transformed so that false special-cause signals are not created. A bounded-physical-situation example is when the time to execute a process cannot be less than zero. When using a log or other transformation, the data alteration needs to make physical sense. For this situation where negative numbers are not possible, a log transformation can be an appropriate physical choice.
The following describes the creation of an individuals control chart as the first step to the formulation of a 30,000-foot-level metric report-out. For this flatness of a part illustration, there is a lower bound of zero.
Individuals Control Chart for Non-normal Data
Transforming individuals control chart data should be an important consideration when providing control charting of individuals data, since an individuals control chart is not robust to non-normality. A data transformation, which makes physical sense, may be necessary for an individuals control chart (i.e., XmR or ImR chart) to adequately assess process stability. The implication of this is that when processes are assessed at a 30,000-foot-level an erroneous decision could be made relative to one of following three considerations (see below), if an appropriate transformation is not made.
Individuals Control Chart Statistical Tracking and Reporting
Three considerations for statistical tracking and reporting of transactional and manufacturing process outputs are:
- Is the process unstable or did something out of the ordinary occur, which requires action or no action?
- Is the process stable and meeting internal and external customer needs? If so, no action is required.
- Is the process stable but does not meet internal and external customer needs? If so, process improvement efforts are needed.
To enhance the process of selecting the most appropriate action or non-action from the three listed reasons, a 30,000-foot-level approach will be used which will include a method to describe process capability/performance reporting in terms that are easy to understand and visualize.
Transforming Individuals Control Chart Data Application Example
Let’s consider a hypothetical application. A panel’s flatness, which historically had a 0.100 inch upper specification limit, was reduced by the customer to 0.035 inches. Consider, for purpose of illustration, that the customer considered a manufacturing nonconformance rate above 1 percent of the specification limit (i.e., 0.100 or 0.035 inches) to be unsatisfactory.
Physical limitations are that flatness measurements cannot go below zero, and experience has shown that common-cause variability for this type of situation often follows a log-normal distribution; i.e., transforming individuals control chart data may later be necessary.
The person who was analyzing the data wanted to examine the process at a 30,000-foot-level view to determine how well the shipped parts met customers’ needs. She thought that there might be differences between production machines, shifts of the day, material lot-to-lot thickness, and several other input variables. Because she wanted typical variability of these inputs as a source of common-cause variability relative to the overall dimensional requirement, she chose to use an individuals control chart that had a daily subgrouping interval. She chose to track the flatness of one randomly-selected, daily-shipped product during the last several years that the product had been produced.
She understood that a log-normal distribution might not be a perfect fit for a 30,000-foot-level assessment, since a multimodal distribution could be present if there were a significant difference between machines, etc. However, these issues could be checked out later since the log-normal distribution might be close enough for this customer-product-receipt point of view.
To model this situation, consider that 1,000 points were randomly generated from a log-normal distribution with a location parameter of two, a scale parameter of one, and a threshold of zero (i.e., log normal 2.0, 1.0, 0). The distribution from which these samples were drawn is shown in Figure 1. A normal probability plot of the 1,000 sample data points is shown in figure 2.
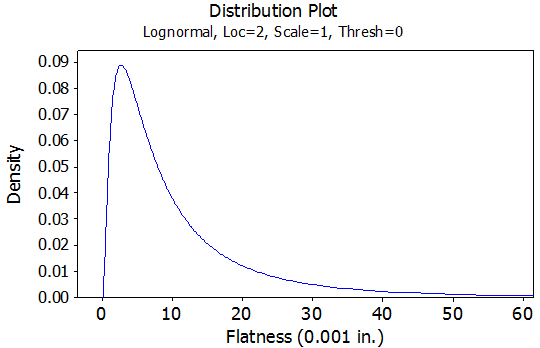
Firgure 1: Distribution from Which Samples Were Selected

Firgure 2: Normal Probability Plot of the Data
From Figure 2, we statistically reject the null hypothesis of normality technically, because of the low p-value, and physically, since the normal probability plotted data do not follow a straight line. This is also logically consistent with the problem setting, where we do not expect a normal distribution for the output of such a process having a lower boundary of zero. A log-normal probability plot of the data is shown in Figure 3.
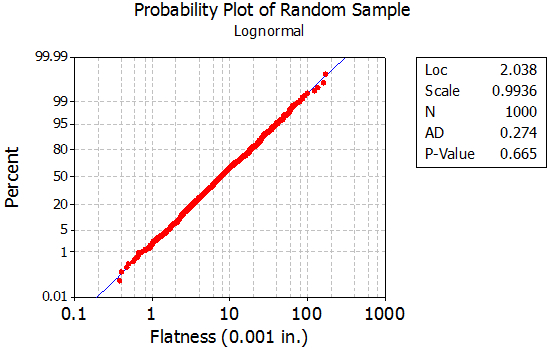
Firgure 3: Log-Normal Probability Plot of the Data
From Figure 3, we fail to statistically reject the null hypothesis of the data being from a log-normal distribution, since the p-value is not below our criteria of 0.05, and physically, since the log-normal probability plotted data tend to follow a straight line. Hence, it is reasonable to model the distribution of this variable as log normal.
If the individuals control chart is robust to data non-normality, an individuals control chart of the randomly generated log-normal data should be in statistical control. In the most basic sense, using the simplest run rule (a point is “out of control” when it is beyond the control limits), we would expect such data to give a false alarm on the average three or four times out of 1,000 points. Further, we would expect false alarms below the lower control limit to be equally likely to occur, as would false alarms above the upper control limit.
Figure 4 shows an individuals control chart of the randomly-generated data.
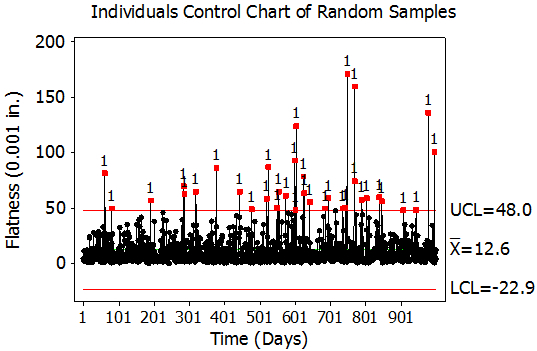
Firgure 4: Individuals Control Chart of the Random Sample Data
The individuals control chart in Figure 4 shows many out-of-control points beyond the upper control limit. In addition, the individuals control chart shows a physical lower boundary of zero for the data, which is well within the lower control limit of -22.9. If no transformation is needed when plotting non-normal data in a control chart, then we would expect to see a random scatter pattern within the control limits, which is not prevalent in the individuals control chart.
Figure 5 shows a control chart using a Box-Cox transformation with a lambda value of zero, the appropriate transformation for log-normally distributed data. This control chart is much better behaved than the control chart in Figure 4. Almost all 1,000 points in this individuals control chart are in statistical control. The number of false alarms is consistent with the design and definition of the individuals control chart control limits.
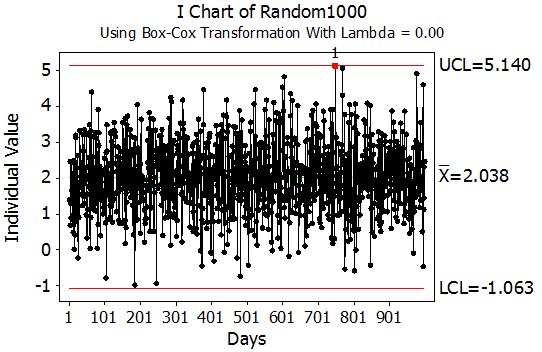
Firgure 5: Individuals Control Chart with a Box-Cox Transformation Lambda Value of Zero
Determining Actions to Take
Previously three decision-making action options were described, where the first option was:
Consideration 1: Is the process unstable or did something out of the ordinary occur, which requires action or no action?
For organizations that did not consider transforming data to address this question, as illustrated in Figure 4, many investigations would need to be made where common-cause variability was being reacted to as though it were special cause. This can lead to much organizational firefighting and frustration, especially when considered on a plant-wide or corporate basis with other control chart metrics.
If data are not from a normal distribution, an individuals control chart can generate false signals, leading to unnecessary tampering with the process. For organizations that did consider transforming data to address this question, as illustrated in Figure 5, there is no overreaction to common-cause variability as though it were special cause.
For the transformed data analysis, let’s next address the other questions:
Consideration 2: Is the process stable and meeting internal and external customer needs? If so, no action is required.
Consideration 3: Is the process stable but does not meet internal and external customer needs? If so, process improvement efforts are needed.
When a process has a recent region of stability, we can make a statement not only about how the process has performed in the stable region but also about the future, assuming nothing will change in the future either positively or negatively relative to the process inputs or the process itself. However, to do this, we need to have a distribution that adequately fits the data from which this estimate is to be made.
For the previous specification limit of 0.100 in., Figure 6 shows a good distribution fit and best-estimate process capability/performance or nonconformance estimate of 0.5 percent (100.0 – 99.5). For this situation, we would respond positively to item number two since the percent nonconformance is below 1 percent; i.e., we determined that the process is stable and meeting internal and external customer needs of a less than 1-percent nonconformance rate; hence, no action is required.
However, from Figure 6 we also note that we expect the nonconformance rate to increase to about 6.3 percent (100 – 93.7) with the new specification limit of 0.35 in. Because of this, we would now respond positively to item number three, since the nonconformance percentage is above the 1-percent criterion. That is, we determined that the process is stable but does not meet internal and external customer needs; hence, process improvement efforts are needed. This metric improvement need would be “pulling” for the creation of an improvement project.
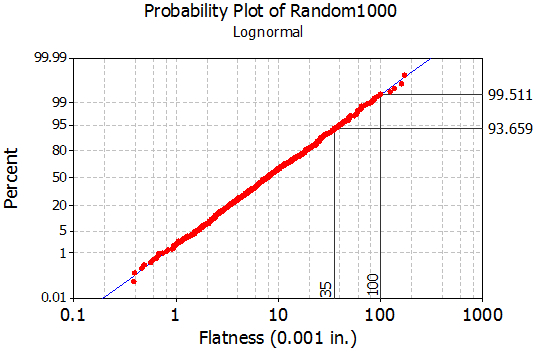
Firgure 6: Log-Normal Plot of Data and Nonconformance Rate Determination for Specifications of 0.100 in. and 0.35 in
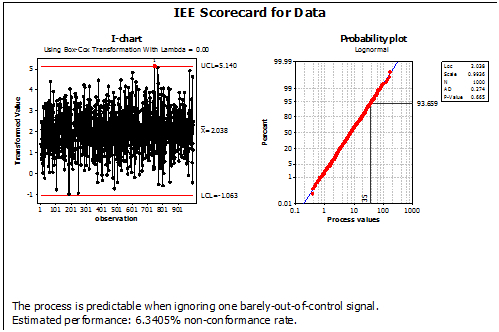
Firgure 7: Predictability Assessment Relative to a Specification of 0.035 inches2
It is important to present the results from this analysis in a format that is easy to understand, such as the 30,000-foot-level metric approach described in Figure 7. With this approach, we demonstrate process predictability using a control chart in the left corner of the report-out and then use, when appropriate, a probability plot to describe graphically the variability of the continuous-response process with its demonstrated predictability statement. With 30,000-foot-level reporting, a statement at the bottom of the plots nets out how the process is performing relative to the new specification requirement of 0.035; i.e., a predictable process with an approximate nonconformance rate of 6.3 percent.
A Lean Six Sigma improvement project could be executed to determine what should be done differently in the process so that the new customer requirements are met. Within this project it might be determined in the analyze phase that there is a statistically significant difference in production machines that now needs to be addressed because of the tightened 0.035 tolerance. This statistical difference between machines was probably also prevalent before the new specification requirement; however, this difference was not of practical importance since the customer requirement of 0.100 was being met at the specified customer frequency level of a less than 1-percent nonconformance rate.
Upon satisfactory completion of an improvement project, the 30,000-foot-level control chart would need to shift to a new level of stability that had a process capability/performance metric that is satisfactory relative to a customer 1 percent maximum nonconformance criterion.
Generalized Statistical Assessment
The specific distribution used in the prior example, log normal (2.0, 1.0, 0), has an average run length (ARL) for false rule-one errors of 28 points. The single sample used showed 33 out-of-control points, close to the estimated value of 28. If we consider a less-skewed log-normal distribution, log normal (4, 0.25, 0), the ARL for false rule-one errors drops to 101. Note that a normal distribution will have a false rule-one error ARL of around 250.
The log-normal (4, 0.25, 0) distribution passes a normality test over half the time with samples of 50 points. In one simulation, a majority, 75 percent, of the false rule-one errors occurred on the samples that tested as non-normal. This result reinforces the conclusion that normality or a near-normal distribution is required for a reasonable use of an individuals chart or a significantly higher false rule-one error rate will occur.
Summary
The output of a process is a function of its steps and input variables. Doesn’t it seem logical to expect some level of natural variability from input variables and the execution of process steps? If we agree to this assumption, shouldn’t we expect a large percentage of process output variability to have a natural state of fluctuation; that is, to be stable?
To me this statement is true for many transactional and manufacturing processes, with the exception of things like naturally auto-correlated data situations such as the stock market. However, with traditional control charting methods, it is often concluded that the process is not stable even when logic tells us that we should expect stability.
Why is there this disconnection between our belief and what traditional control charts tell us? The reason is that often underlying control-chart-creation assumptions are not valid in the real world. Figures 4 and 5 illustrate one of these points where an appropriate data transformation is not made.
The questions that should be addressed when tracking a process can be expressed as determining which actions or non-actions are most appropriate.
- Is the process unstable or did something out of the ordinary occur, which requires action or no action?
- Is the process stable and meeting internal and external customer needs? If so, no action is required.
- Is the process stable but does not meet internal and external customer needs? If so, process improvement efforts are needed.
This article described why appropriate transformations from a physical point of view need to be a part of this decision-making process.
The statement at the bottom of Figure 7 describes the state of the examined process in terms that everyone can understand; i.e., the process is predictable with an estimate 6.3-percent nonconformance rate.
Benefiting from Application of 30,000-foot-level Predictive Performance Metric throughout Organizations
An organization gains much when this form of scorecard-value-chain reporting is used throughout its enterprise and is part of its decision-making process and improvement project selection. A system for accomplishing this objective is Integrated Enterprise Excellence (IEE).
Eight application examples of converting traditional dashboards and scorecards to 30,000-foot-level reporting is available in the article Predictive Performance Reporting, where more insight is gained from this reporting format.
An IEE Business Management System for scorecard reporting addresses the common place issues that are described in a 1-minute video:
Easy Creation of 30,000-foot-level Report-outs
A free app to create 30,000-foot-level reports is available through the link
References
- Forrest W. Breyfogle III, Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Bridgeway Books/Citius Publishing, 2008
- Figure created using Enterprise Performance Reporting System (EPRS) Software
Contact Us to set up a time to discuss with Forrest Breyfogle how your organization might gain much from an Integrated Enterprise Excellence (IEE) Business Process Management System and its 30,000-foot-level reporting.

