There are major issues with AQL that need to be understood by those involved with Acceptable Quality Level inspections. A 30,000-foot-level process metric report-out has many advantages over AQL testing.
Acceptable Quality Level (AQL), which provides a sample size to determine if a lot should be accepted or rejected, statistically does not protect customer. Sampling plans are typically determined from tables as a function of an AQL criterion and other characteristics of the lot. Pass/fail decisions for an AQL-evaluated lot are based only on the lot’s performance, not on previous product performance from the process. AQL sampling plans do not give a picture of how a process is performing.
Acceptable Quality Level (AQL) Issues
Content of this webpage is from Chapter 21 of Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Forrest W. Breyfogle III.
AQL sampling plans are inefficient and can be very costly, especially when high levels of quality are needed. Often, organizations think that they will achieve better quality with AQL sampling plans than is possible. The trend is that organizations are moving away from AQL sampling plans; however, many organizations are slow to make the transition. The following describes the concepts and shortcomings of AQL sampling plans.1
When setting up an AQL sampling plan, much care needs to be exercised in choosing samples. Samples must be a random sample from the lot. This can be difficult to accomplish. Neither sampling nor 100% inspection guarantees that every defect will be found. Studies have shown that 100% inspection is at most 80% effective.
There are two kinds of sampling risks:
- Good lots can be rejected.
- Bad lots can be accepted.
The operating characteristic (OC) curve for sampling plans quantifies these risks. Figure 1 shows an ideal operating curve.

Figure 1: Ideal OC Curve
Because an ideal OC curve is not possible, OC curves are described using the following terms:
Acceptable Quality Level (AQL)
- AQL is typically considered to be the worst quality level that is still considered satisfactory. It is the maximum percent defective that for purposes of sampling inspection can be considered satisfactory as a process average.
- The probability of accepting an AQL lot should be high. A probability of 0.95 translates to a a risk of 0.05.
Rejectable Quality Level (RQL)
- This is considered to be unsatisfactory quality level.
- This is sometimes called lot tolerance percent defective (LTPD).
- This consumer’s risk has been standardized in some tables as 0.1.
- The probability of accepting an RQL lot should be low.
Indifference Quality Level (IQL)
- Quality level is somewhere between AQL and RQL.
- This is frequently defined as quality level having probability of acceptance of 0.5 for a sampling plan.
An OC curve describes the probability of acceptance for various values of incoming quality. Pa is the probability that the number of defectives in the sample is equal to or less than the acceptance number for the sampling plan. The hyper-geometric, binomial, and Poisson distributions describe the probability of acceptance for various situations.
The Poisson distribution is the easiest to use when calculating probabilities. The Poisson distribution can often be used as an approximation for the other distributions. The probability of exactly x defects [P(x)] in n samples is
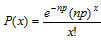
For “a” allowed failures, P(x≤a ) is the sum of P(x) for x = 0 to x = a.
Figure 2 shows an AQL operating characteristic curve for an AQL level of 0.9%. Someone who is not familiar with the operating characteristic curves of AQL would probably think that passage of this AQL 0.9% test would indicate goodness. Well this is not exactly true because from this operating curve (OC) it can be seen that the failure rate would have to be actually about 2.5% to have a 50%/50% chance of rejection.
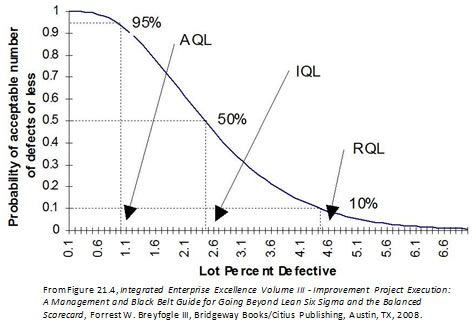
Figure 2: An operating characteristic curve. N=150, c=3.
AQL sampling often leads to activities that are associated with attempts to test quality into a product. AQL sampling can reject lots that are a result of common-cause process variability. When a process output is examined as AQL lots and a lot is rejected because of common-cause variability, customer quality does not improve.
Example that highlights issues with AQL testing
For N (lot size) = 75 and AQL = 4.0%, ANSI/ASQC Z1.4-1993 (Cancelled MIL-STD-105) yields, for a general inspection level II, a test plan in which
- Sample size = 13
- Acceptance number = 1
- Rejection number = 2
From this plan we can see how AQL sampling protects the producer. The failure rate at the acceptance number is 7.6% [i.e., (1/13)(100) = 7.6%], while the failure rate at the rejection number is 15.4% [i.e., (2/13)(100) = 15.4%].
Usually a sample size is considered small relative to the population size if the sample is less than ten percent of the population size. In this case, the population size is 75 and the sample size is 13; i.e., 13 is greater than 10% of the population size. However, for the sake of illustration, let’s determine the confidence interval for the failure rate for the above two scenarios as though the sample size relative to population size were small. This calculation yielded:
Test and Confidence Interval for One Proportion
Test of p = 0.04 vs p < 0.04
95% Upper Exact
Sample X N Sample p Bound P-Value
1 1 13 0.076923 0.316340 0.907
Test and Confidence Interval for One Proportion
Test of p = 0.04 vs p < 0.04
95% Upper Exact
Sample X N Sample p Bound P-Value
1 2 13 0.153846 0.410099 0.986
For this AQL test of 4%, the 95% confidence bound for one failure is 31.6% and for two failures is 41.0%. Practitioners often don’t realize how these AQL assessments do not protect the customer as much as they might think.
This example illustrates how a test’s uncertainty can be very large when determining if a lot is satisfactory or not. A lot sample size to adequately test the low failure rate criteria in today’s products is often unrealistic and cost prohibitive. To make matters worse, these large sample sizes would be needed for each test lot.
Does AQL testing answer the wrong (not best) question?
With AQL testing, sampling provides a decision-making process as to whether a lot is satisfactory or not relative to a specification; however, this is often a very difficult, if not impossible, task to accomplish. When one is confronted with the desire to answer a question that is not realistically achievable, we should first step back to determine whether we are attempting to answer the wrong (or at least not the best) question. Sometimes we might be wasting much resource attempting to answer the wrong question with much accuracy; e.g., to the third decimal place.
When we are examining an AQL sample lot of parts, population statements are being made about each lot. However, in most situations, a lot could be considered a time series sample of parts produced from the process. With this type of thinking, our sampling can lead to a statement about the process that produces the lots of parts. With this approach, our sample size is effectively larger since we would be including data in our decision-making process from previous sampled lots.
Scoping the situation using this frame of reference has another advantage. If a process non-conformance rate is unsatisfactory, the statement is made about the process, not about an individual lot. The customer can then state to its supplier that the process needs to be improved, which can lead to specific actions that result in improved future product quality. This does not typically occur with AQL testing since focus in lot sampling is given to what it would take to get the current lot to pass the test. For this situation, it might end up being, without the customer knowing it, a resample of the same lot. This second sample of the same lot could pass because of the test uncertainty, as described earlier.
When determining an approach for assessing incoming part quality, the analyst needs to address the question of process stability. If a process is not stable, the test methods and confidence statements cannot be interpreted with much precision. Process control charting techniques can be used to determine the stability of a process.
Consider also what actions will be taken when a failure occurs in a particular attribute-sampling plan. Will the failure be “talked away”? Often, no knowledge is obtained about the “good” parts. Are these “good parts” close to “failure”? What direction can be given to fixing the source of failure so that failure will not occur in a customer environment? One should not play games with numbers! Only tests that give useful information for continually improving the manufacturing process should be considered.
Fortunately, however, many problems that are initially defined as attribute tests can be redefined to continuous response output tests. For example, a tester may reject an electronic panel if the electrical resistance of any circuit is below a certain resistance value. In this example, more benefit could be derived from the test if actual resistance values are evaluated. With this information, percent of population projections for failure at the resistance threshold could then be made using probability plotting techniques. After an acceptable level of resistance is established in the process, resistance could then be monitored using control chart techniques for variables. These charts then indicate when the resistance mean and standard deviation are decreasing or increasing with time, an expected indicator of an increase in the percentage builds that are beyond the threshold requirement.
Additionally, Design of Experiments (DOE) techniques could be used as a guide to manufacture test samples that represent the limits of the process. This test could perhaps yield parts that are more representative of future builds and future process variability. These samples will not be “random” from the process, but this technique can potentially identify future process problems that a random sample from an initial “batch” lot would miss.
With the typical low failure rates of today, AQL sampling is not an effective approach to identify lot defect problems.
Alternative Methodology to AQL Testing
In lieu of using AQL sampling plans to periodically inspect the output of a process, more useful information can be obtained by using 30,000-foot-level Reports with Predictive Measurements to address process common-cause and special-cause conditions. Process capability/performance studies can then be used to quantify the process common-cause variability. If a process is not capable, something needs to be done differently to the process to make it more capable.
30,000-foot-level Charting Applications
The described 30,000-foot-level charting technique has many applications, as described in 30,000-foot-level Performance Reporting Applications.
The Integrated Enterprise Excellence (IEE) Business Management System with its 30,000-foot-level reporting in an organization addresses the common place organizational scorecard and improvement issues that are described in a 1-minute video:
30,000-foot-level charting can reduce the firefighting that can occur with traditional business scorecarding systems.The Integrated Enterprise Excellence (IEE) business management system uses 30,000-foot-level charting to address these issues.

References
- Forrest W. Breyfogle III, Integrated Enterprise Excellence Volume III – Improvement Project Execution: A Management and Black Belt Guide for Going Beyond Lean Six Sigma and the Balanced Scorecard, Bridgeway Books/Citius Publishing, 2008
Contact Us to set up a time to discuss with Forrest Breyfogle how your organization might gain much from an Integrated Enterprise Excellence (IEE) Business Process Management System and how 30,000-foot-level reporting can resolve AQL inspection issues.

